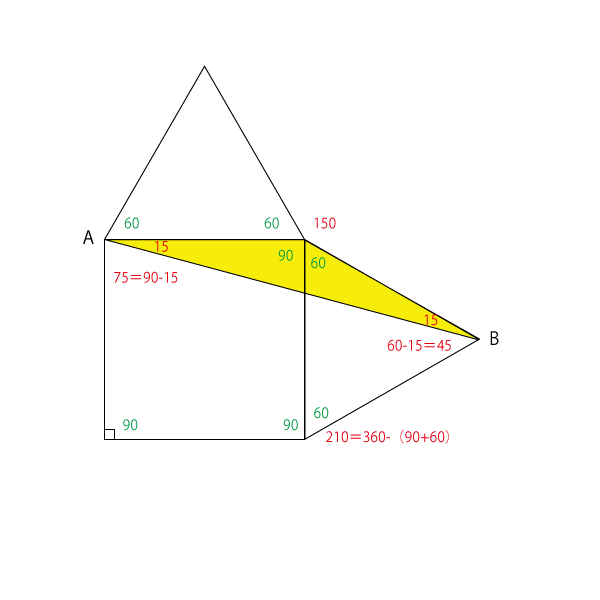
例1)正三角形や正方形を組み合わせた問題 下の図で四角形ABCDが正方形、三角形CEDが正三角形のときアの角度を求める CE=CDになるので 三角形CDEが二等辺三角形になる ことに着目 ∠CDEを求める (180−30)÷2=75° よってアの角度h 9075=15° と求めることが出来る。 等しい長さの辺を探して二等辺三角形を探すようにして問題を解いてみましょう。长方形 S=ab C=(ab)×2 正方形 S=aa 或 对角线×对角线÷2 C=4a 平行四边形 S=ah 三角形 S=ah÷2 梯形 S=(ab)×h÷2 圆形 S=πrr C=πd 椭圆 S=πrr 平面图形 名称 符号 周长C和面积S 正方形 a—边长 C=4a S=a2 长方形 a和b-边长 C=2(ab) S=ab 三角形 a,b,c-三边长 h-a边上的高 s-周长的一半 ・∠afbは三角形afbのひとつの頂点ですから、180°-(∠fab+∠fba)であることも明白です。 ・∠fabと∠fbaは共に正三角形のひとつの角(60°)を二つに分けた一つですから・・・ ∠dfa = ∠fab+∠fba =60°= ∠bdc+∠fba = ∠dca
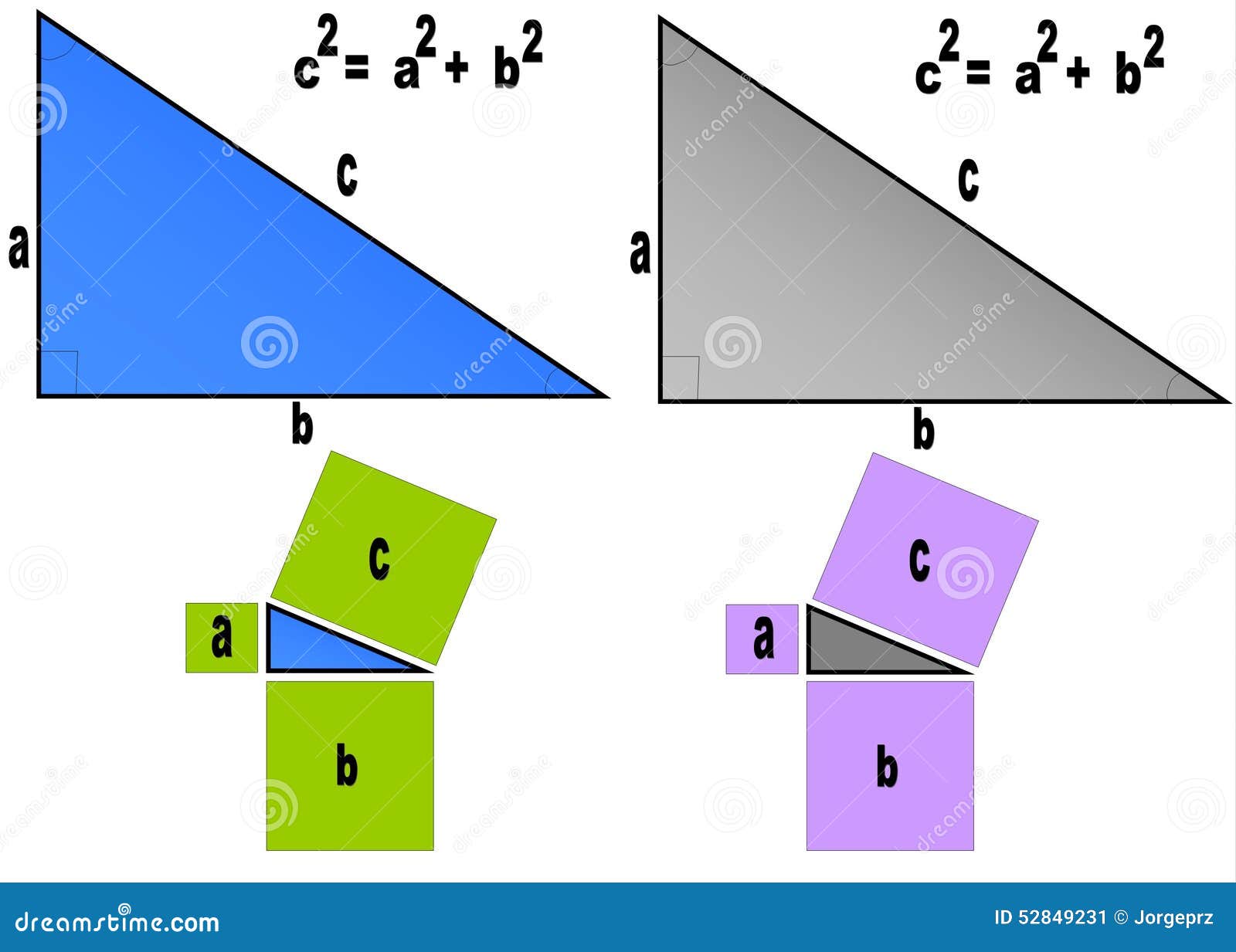
毕达哥拉斯定理库存例证 插画包括有
正方形 正三角形 組み合わせ 角度
正方形 正三角形 組み合わせ 角度- 扩展资料 (1)长方形的四个角都为90°。 (2)长方形的两组对边分别平行且长度相等。 (3)长方形的两条对角线长度相等。 若S为正方形的面积,l为正方形的周长,长方形的长为a,宽为b,c为正方形的对角线则:S=a*b、l=2* (ab)、c=√ (a^2b^2 你对这个回答的 方法/步骤 1/7 分步阅读 打开ppt13文档 2/7 在页面中插入一个三角形 ps教程图片手把手教你ps教程图片,3天内不满意可退款 广告 3/7 点击三角形,点击鼠标右键选择"设置形状格式"



正三角形の角度 正方形 ひし形との融合問題を解説 数スタ
ア=78°。 (4) (5) ア6330=93°。 アイ==135°。 ア=イ=135÷2=675°。 ウ180()45=1275°。 解答:(1)ア58° イ98° (2)60° (3)78° (4)93° (5)ア、イ675° ウ1275° 在python二级考试中,有要求绘画简单图形的编程题。以下分享一些简单图形的绘制代码绘制边长为100的正方形,import turtled = 0for i in range(4) #图形边数 turtlefd(0) #边长 d = d90 #旋转角度 turtleseth(d)绘制等边三角形import turtled 回答量: 871 采纳率: 63% 帮助的人: 461万 我也去答题 访问个人页 关注 展开全部 双击线条,在打开的对话框左下角"plot type"中选择Linesymbol。 选了后,在右边就可以选择标志形状。 这种做法是对整条线进行统一操作,如要想更改线中某一个点的标志形状,参见time_resolved前半
入試解説 6年生 男子校 5年生 正方形 正三角形 東京 兵庫 灘 算数オリンピック 共学校 面積比 円 図形NOTE logix出版 角度 1日目 女子校 直角三角形 4年生 相似 立方体 長方形 おうぎ形 30度 正六角形 16年 17年 19年 トライアル 18年 年 二等辺三角形 直角二等辺三角形 立体の切断 ファイナル 21年 15年 図形の移動 共通部分 大阪 12年 13年 面積の和 ジュニア 展開図 初中数学 正方形外做等边三角形, 求角度数 上传于 优酷热门 电视剧 电影 综艺 音乐 少儿 资讯 纪录片 公益 体育 汽车 科技 财经 娱乐 文化 动漫 旅游 时尚 亲子 教育 游戏 会员 发现 片库 电视剧 电影 综艺 音乐 少儿 资讯 纪录片 公益 体育 汽车・正三角形(面積から辺と高さ) 正三角形の面積から1辺の長さと高さを計算します。 直角三角形 ・ 直角三角形(底辺と高さ) 直角三角形の底辺と高さから、斜辺と角度と面積を計算します。
在边长为 1 的正方形中随机取三个点,构成三角形的面积期望是多少? 问题来源:CodeVS 交流群 自己重写了验证程序,答案确实在 0076 左右。 另外,随机选取点的方式是: (x=rand 0,1,y=rand因为正方形里面有 2个三角形 三角形的内角加起来是 180° 正方形则是 360° 正三角形内角: (n−2)×180°/n=180°/3=60°; 正四边形内角: (n−2)×180°/n=2×180°/4=90°; 正五边形内角: (n−2)×180°/n=3×180°/5=108°; 正六边形内角: (n−2)×180°/n=4×180°/6=1°;



Pqrs是正方形 Poq是等边三角形 角度sor的值是多少 教育小本子




毕达哥拉斯定理库存例证 插画包括有
正三角形のある頂点から角の二等分線を下ろすと、合同な \(2\) つの直角三角形ができます。 この直角三角形は、角度が必ず「\(\color{red}{30^\circ, 60^\circ, 90^\circ}\)」となり、辺の比は「\(\color{red}{1 \sqrt{3} 2}\)」となります。三角形の3辺から角度を計算 答えの度分秒(° ′ ″ )は、秒の小数点以下2桁まで求めています。 台形型の部屋の変形のコーナーに壁にピッタリと合った棚を作ろうと思い図面を牽きましたが角度の算出方法が分からずお世話になりました、凄く助かり正方形 正三角形 正六角形 正多角形 角の大きさ(度) 正多角形 角の大きさ(度) 正五角形 108 正十八角形 160 正八角形 135 正二十角形 162 正九角形 140 正二十四角形 165 正十角形 144 正三十角形 168 正十二角形 150 正三十六角形 170



Q Tbn And9gctmkiqk 1u R2dcluyxq7onwzqe7rz5tts5jps7h39vn Y22n Usqp Cau




例題 正方形 已知邊長求正方形內三角形 Youtube
正三角形(せいさんかくけい、英 equilateral triangle )は、正多角形である三角形である。 つまり、3本の辺の長さが全て等しい三角形である。 3つの内角の大きさが全て等しい三角形と定義してもよい。 1つの内角は 60°(π/3 rad)である。 また一つの内角が正三角形角度为60° 正六边形角度为1° (1)6块正三角形,0块正六边形 (2)4块正三角形,1块正六边形 (3)2块正三角形,2块正六边形 (4)0块正三角形,3块正六边形 有4种方案 单独使用正三角形、正方形、正六边形、正八边形四种地砖,不能镶嵌(密铺)地面的是三角形 1° 100 033 正方形 90° 100 025 五角星 144° 100 04 正六边形 60° 100 0167




如何计算角度 8 步骤 包含图片



初中 彻底度量345三角形 345三角形的精确角度 精作网
方法一:作圆,以半径为长度单位(半径即是所求正六边形边长),划分圆,并连接各分点,即是所求正六边形。 方法二: 以任意长画一条线段AB。 以A为圆心,AB为半径,作圆A。 以B为圆心,AB为半径,作圆B与圆A交于点C。 连接AC,BC。 三角形ABC为等边三角形。 在AB上取 三等分点 M。 在AC和BC上分别取点N,O,使CN=AM=OB。_____ 因为任意n边形内角和180(n2) n≥3且为自然数 正n边形各内角为180(n2)÷n n≥3且为自然数 原因因为任意n边形外角和总为为360度,一个内角和一个外角和为180度,n边形有n对内角外角,所以有任意n边形内角和180(n2) n≥3且为自然数二等辺三角形の角度の求め方 厳選6問解説! 正三角形の角度 正方形、ひし形との融合問題を解説! 平行四辺形とひし形の違いってなに?? 平行四辺形の角度、辺の長さを求める問題を解説! 平行四辺形の中から面積の等しい三角形を見つける問題を徹底




正三角形高求正三角形的高 Utvos




老师熬夜整理 初中数学最全几何模型大汇总 学生大呼 过瘾
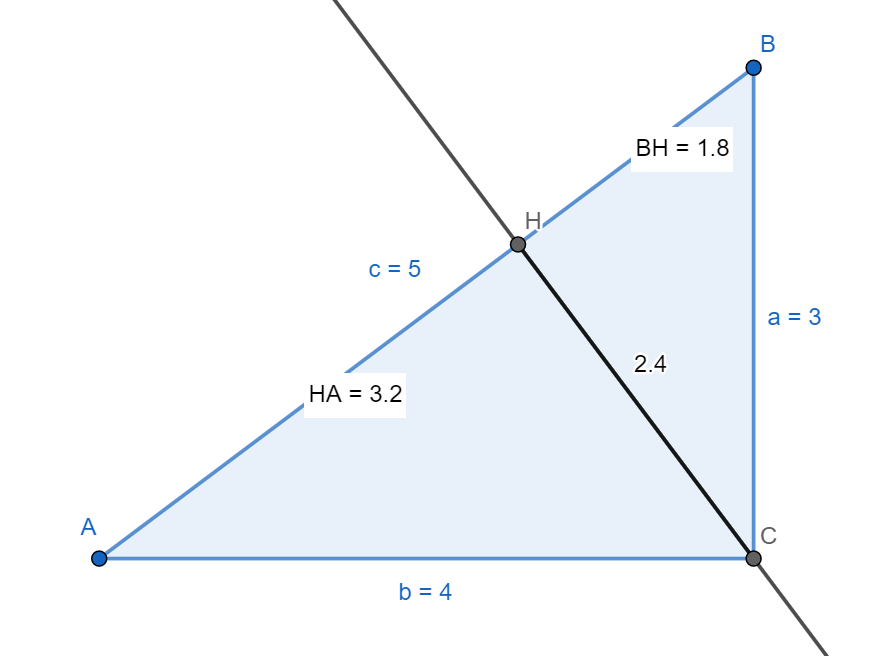
右図のように,直線CHをかくと,三角形DHCは正三 角形になります。 イ=60°なので, ×2=90°-60°=30° =30°÷2=15° ア=180°-(15°+90°)=75° 《2.等しい角を使って》 右の図は二等辺三角形で, 印をつけた角の大きさは等しいです。アの角の 举报 收起 匿名用户 展开全部 设正方形边长为x。 因为以6 和 4 为斜边的直角三角形相似,所以x/6=根号(4的平方x的平方)除以4 解方程得x的平方为144/13 即正方形的面积入試解説 6年生 男子校 5年生 正方形 正三角形 東京 兵庫 灘 算数オリンピック 共学校 面積比 円 図形NOTE logix出版 角度 1日目 女子校 直角三角形 4年生 相似 立方体 長方形 おうぎ形 30度 正六角形 16年 17年 19年 トライアル 18年 年 二等辺三角形 直角二等辺三角形 立体の切断 ファイナル 21年 15年 図形の移動 共通部分 大阪 12年 13年 面積の和 ジュニア 展開図



正方形に内接する正三角形 算数解法の極意




怎么计算角度 生活百科
正三角形の融合パターン ABC、 ADEが正三角形のとき、 ∠x の大きさを求めなさい。 解説&答えはこちら 答え ∠x=35° まず、 ABCの正三角形に注目すると 1つの角は60°になることから 赤い部分が35°になることがわかります。 次は ADEの正三角形に注目すると731 梁的合理截面形状 矩形优于正方形,正方形优于圆形,工字形比矩形截面更为合理。 在设计梁时,一方面要使梁具有足够的强度,以保证梁能够安全正常地工作;另一方面又要使梁的材料充分发挥其作用,以便节省材料,尽可能提高梁的弯曲强度。一、矩形、菱形、正方形的性质 1矩形的性质 ①具有平行四边形的一切性质; ②矩形的四个角都是直角; ③矩形的对角线相等; ④矩形是轴对称图形,它有两条对称轴; ⑤直角三角形斜边上的中线等于斜边




老师熬夜整理 初中数学最全几何模型大汇总 学生大呼 过瘾



2
直角三角形知道一条边长和一个角度,利用三角函数可以计算出另外两条边的长度。 1个三角形,其中一个角是90度另外一个角是30度,一条短边是23CM,求其它2条边长度 其实这题有好多解,如果再加个条件就有确定答案当他为45度直角三角形时,三边比为1根号2 1当他三角形 面积 = ½ × 底 × 高 b = 底 h = 垂直高度 正方形 面积 = a 2 a = 边长 矩(长方)形 面积 = 宽 × 高 w = 宽 h = 高 平行四边形 面积 = b × h b = 底 h = 垂直高度 梯形 面积 = ½(a b) × h h =垂直高度 圆形 面积 = π × r 2 周长 = 2 × π × r r = 半径 椭圆形 面积 = π ab 扇形 面积 = ½ × r 2 × θ r =半径Right triangle (1) cosθ = a c , sinθ= b c , tanθ= b a (2) P ythagorean theorem a2b2 =c2 R i g h t t r i a n g l e ( 1) cos θ = a c , sin θ = b c , tan θ = b a ( 2) P y t h a g o r e a n t h e o r e m a 2 b



竞赛试题 矩形内接正三角形问题 思路
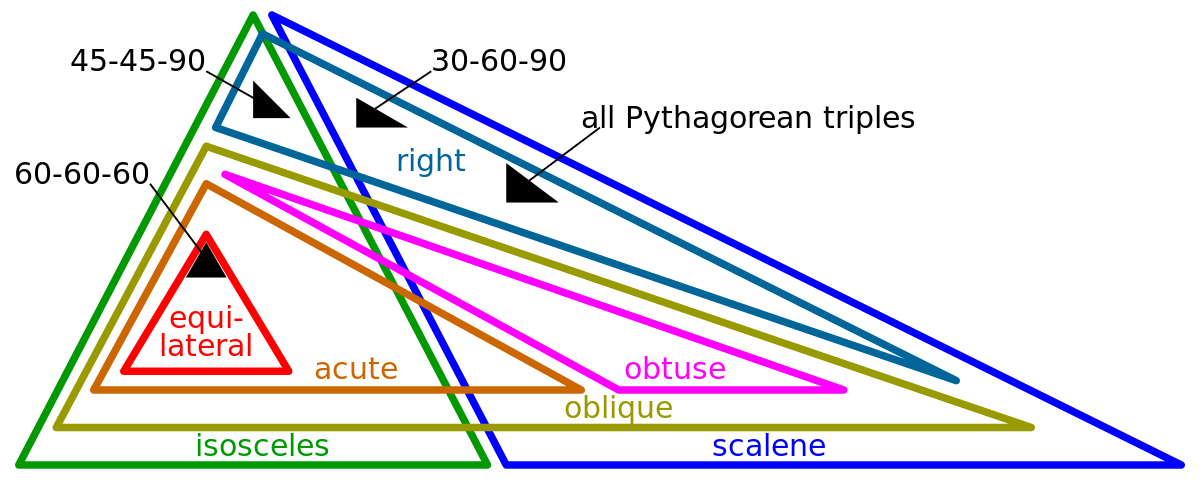



特殊直角三角形 维基百科 自由的百科全书




正三角形高求正三角形的高 Utvos




難問 角度 二等辺三角形 正三角形 下京中 中野 豊司 Youtube



三角形的外接圓與外心角度 Live 多媒體數學觀念典online




怎么计算角度 生活百科



正方形边长为1 求角度x和三角形的周长 需要一点勇气 哔哩哔哩 つロ干杯 Bilibili



用作高法根据特殊角度构造直角三角形 知乎



密铺 搜狗百科




怎么计算角度 生活百科



巧用图形对称性探求正方形线段及角度关系 西湖数论之我来讲题 第184期 西湖数论 微信公众号文章阅读 Wemp



透视平面镶嵌问题 7 4课题学习 初中人教版 数学中国网



三角形边长公式和图解 信息评鉴中心 酷米资讯 Kumizx Com



1




正方形 维基百科 自由的百科全书



竞赛试题 矩形内接正三角形问题 思路
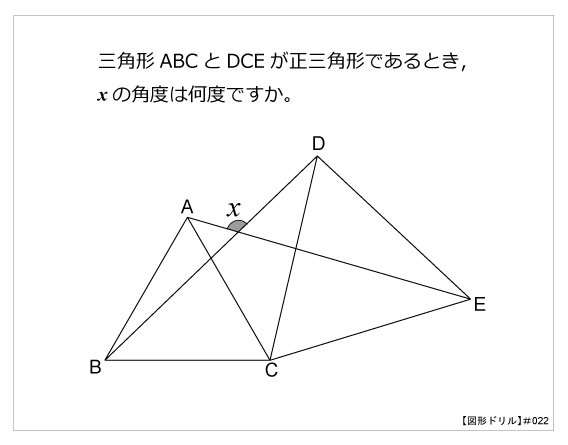



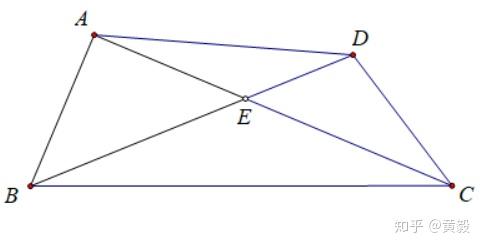
図形ドリル 第22問 正三角形の回転合同 算数星人のweb問題集 中学受験算数の問題に挑戦
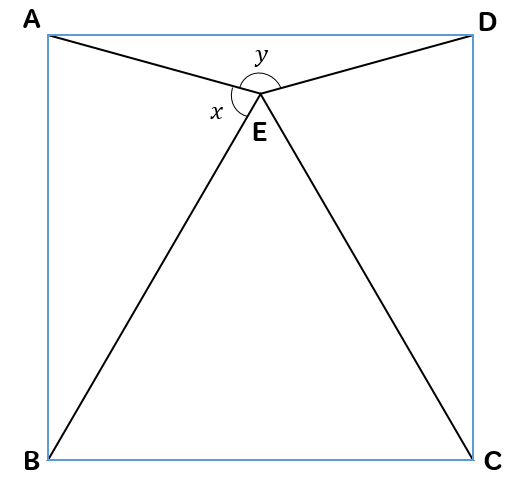



正三角形の角度 正方形 ひし形との融合問題を解説 数スタ
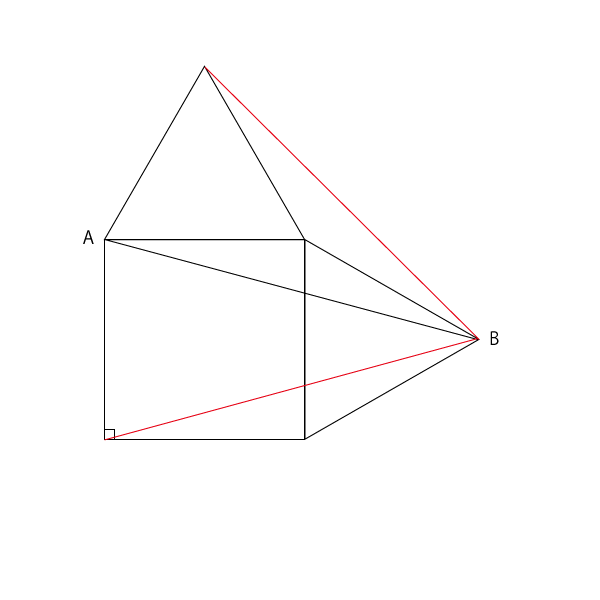



正方形と正三角形が組み合わさった図形の面積計算 受験算数入門




数学 中2 70 正三角形 Youtube




いろいろな角度を求める問題1 図形の等辺を利用する 中学受験準備のための学習ドリル




正方形有几条对称轴 解历史



初中数学中考几何证明题 不知大家有没有更简单的方法 哔哩哔哩 つロ干杯 Bilibili




老师熬夜整理 初中数学最全几何模型大汇总 学生大呼 过瘾



直角三角形 图片欣赏中心 急不急图文 Jpjww Com



1



第84問の解答



巧用图形对称性探求正方形线段及角度关系 西湖数论之我来讲题 第184期 西湖数论 微信公众号文章阅读 Wemp



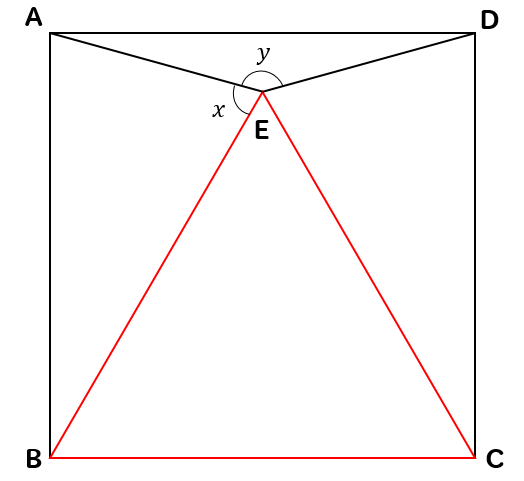
观察下面图形 回答下列问题 1 从数学的角度描述图形一的两个特征 第一 等边三角形三条边都相等 三个角都是60度第二 正方形 的4条边都相等 4个角都是90度 2 从数学角度描述图形一与图形二的一个相同特征 相同特征 都有相等的边 都是轴对称图形 对称轴都交于一点



4 2 重なった正方形 正三角形から角度を求めるには さんすうがく



1



図の問題がわかりません 正三角形と正方形を組み合わせた図形で Yahoo 知恵袋
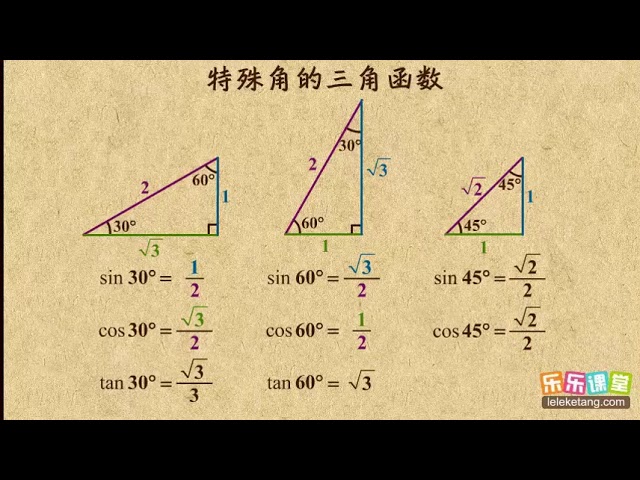



02特殊角的三角函数直角三角形的边角关系初中数学初三 Youtube




五种方法解决一道几何经典题 无数同学表示伤不起 三角形 正三角形 构造 正方形 网易订阅




動画追加 第29回 平面図形 6年生 差がつきやすい問題 日能研の歩き方



三角形内弦图和外弦图 万图壁纸网



八年级上学期培优专题 旋转变换与全等三角形 中学数学培优竞赛 微信公众号文章阅读 Wemp




3种方法来求直角三角形斜边的长度



補助線の練習




Laq ラキューピンク7種 正方形 正三角形 ひょうたん形大小 1 角度付き 三方つなぎ 90 用 計0ピース フリーパステルカラー 日本代購代bid第一推介 Funbid



直角三角形 图片欣赏中心 急不急图文 Jpjww Com



七种最常用的音响摆位方法 山东军兴影音科技有限公司




如何计算角度 8 步骤 包含图片




3种方法来求三角形的第三个角




如何利用编程机器人程小奔编程玩几何 Makeblock



正方形不同角度图片 第2页 要无忧健康图库
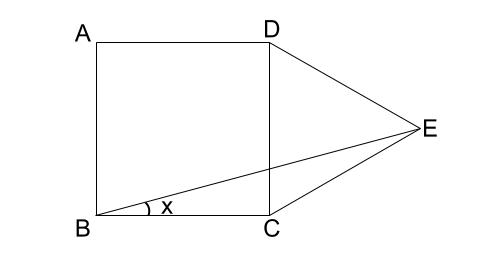



中学数学 正三角形 中学数学の無料オンライン学習サイトchu Su



三角形的角度的总和 上的三角形的角度之和的定理



正方形と正三角形 聖望中学 2010年 どう解く 中学受験算数



スウガクとくガウス ラングレーの問題




正三角形高求正三角形的高 Utvos
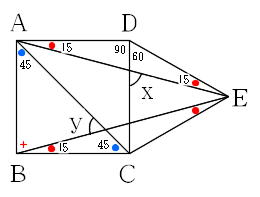



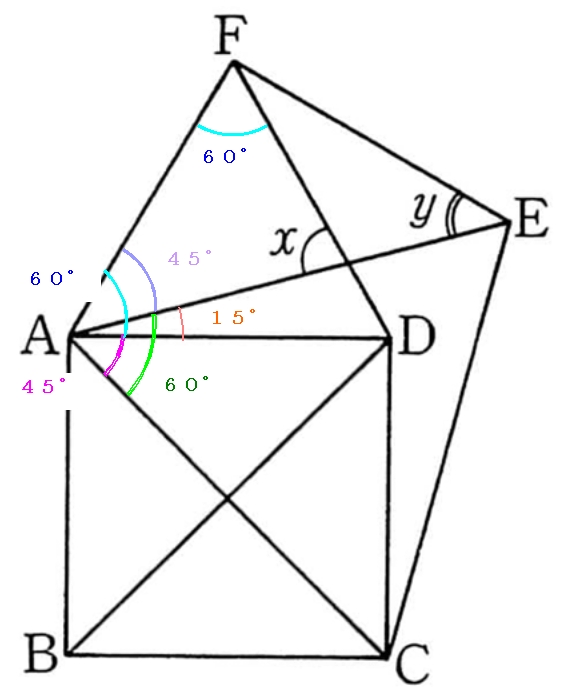
Mathematics 算数のコツ 1 角度の問題は 等しい角を見つけて書き込む 働きアリ
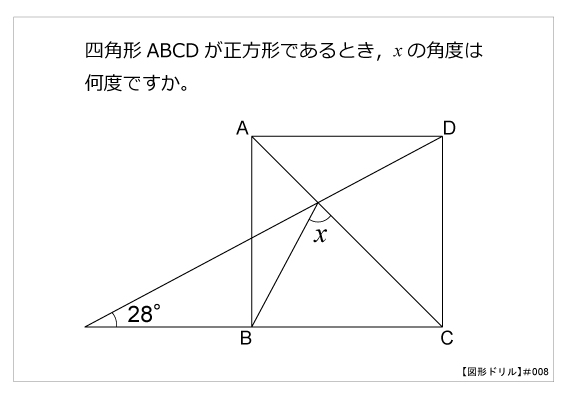



図形ドリル 第8問 正方形と角度 算数星人のweb問題集 中学受験算数の問題に挑戦



适合八九年级 常考的几何动态题 三角形与四边形 12 正方形与等腰直角三角形 旋转 自由微信 Freewechat



三角形内弦图和外弦图 万图壁纸网



初中数学 正方形中证明线段的数量关系 要利用旋转证明三角形全等 哔哩哔哩 つロ干杯 Bilibili




小学5年生 合同な図形 解説を見ても分かりません みなさん今晩は 数学 教えて Goo
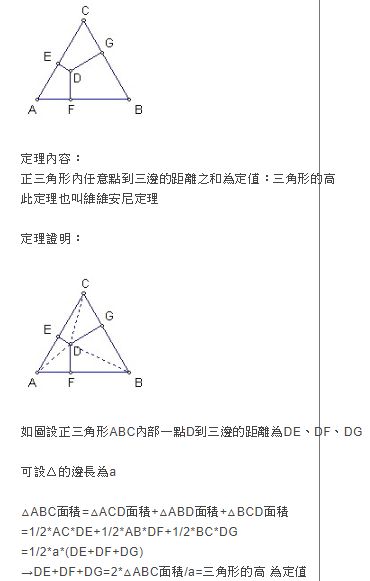



三邊長為的三角形面積是多少阿摩 阿摩線上測驗



正6边形内角度数 正6边形内角度数总和 正112边形内角度数



正方形と正三角形が組み合わさった図形の面積計算 受験算数入門



補助線の練習



直角三角形 图片欣赏中心 急不急图文 Jpjww Com



入試に使える算数の基礎 角度の問題



如何快速在cad中画出等边三角形 知乎




五种方法解决一道几何经典题 无数同学表示伤不起 三角形 正三角形 构造 正方形 网易订阅




一般 正三角形的高與面積 Youtube
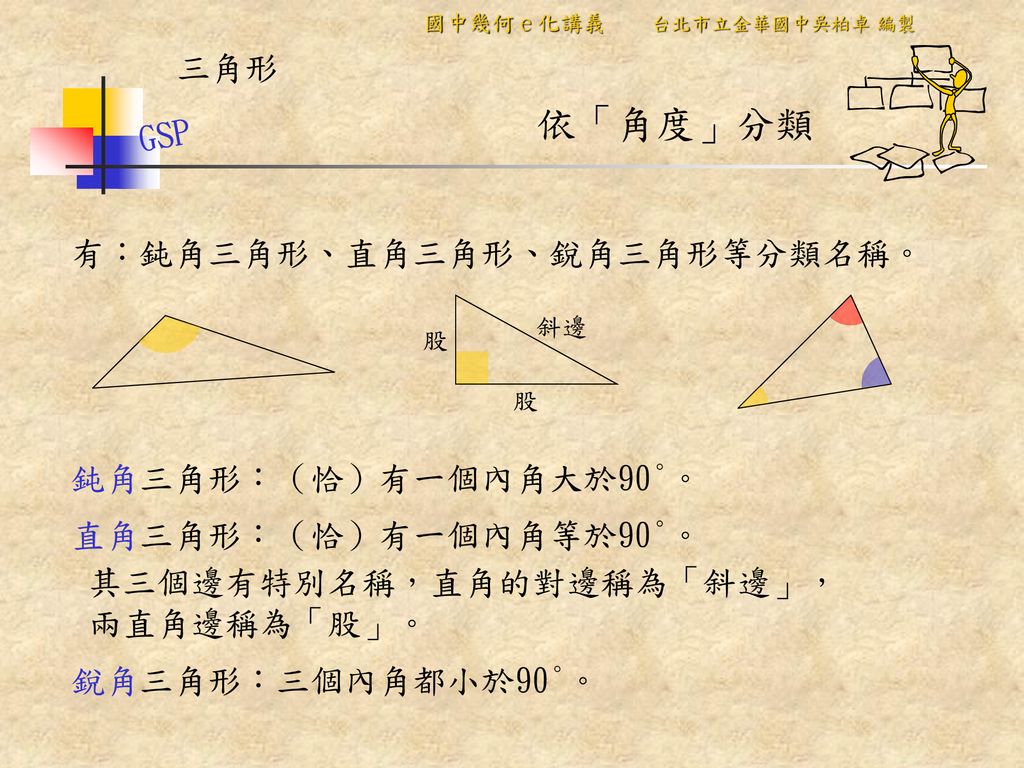



簡要說明常見到的三角形基本性質大致上有 1 與角度有關的等量關係 外角和 內角和 外角定理 2 邊長不等關係 兩邊和大於第三邊 兩邊差小於第三邊



如图1 把边长为4的正三角形各边分成四等分 连结各分点得到16个小正三角形 小题1 如图2 连结小正三角形 的顶点得到一个正六边形abcdef 初中一年级 数学试题 相似多边形的性质考点 相似三角形的判定考点 相似三角形的性质考点 相似三角形的应用考点 好技网




正三角形面積公式小學正方形 長方形 三角形 梯形 平行四邊形的面積 Chris Cold



正方形と二等辺三角形の問題です 角度xを出し方をお教えください 宜しく Yahoo 知恵袋




正三角形の角度 正方形 ひし形との融合問題を解説 数スタ




基本繪圖 畫出基本圖形 正三角形 詩娟的交流花園 痞客邦




いろいろな角度を求める問題1 図形の等辺を利用する 中学受験準備のための学習ドリル



正方形の中の正三角形以外の部分の和は 11年 城北中学 算数解法の極意
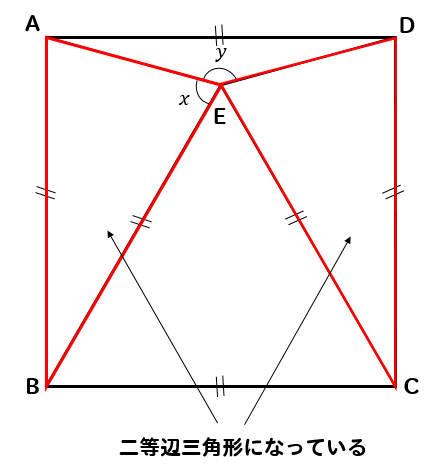



正三角形の角度 正方形 ひし形との融合問題を解説 数スタ




五种方法解决一道几何经典题 无数同学表示伤不起 三角形 正三角形 构造 正方形 网易订阅
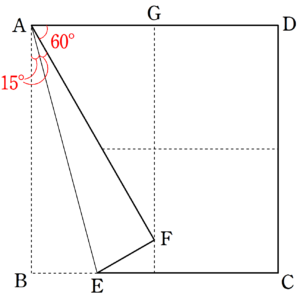



折り紙で正三角形を作る Fukusukeの数学めも



七种最常用的音箱摆位方法




11 3 三角函数 Acionscript3 0 教程



名師課輔網 正 餘弦定理



直角三角形三条边是3 图片欣赏中心 急不急图文 Jpjww Com




正三角形高求正三角形的高 Utvos




正三角形の角度 正方形 ひし形との融合問題を解説 数スタ




正三角形 维基百科 自由的百科全书



直角三角形 图片欣赏中心 急不急图文 Jpjww Com




初中几何 正方形与对称 旋转 2



竞赛试题 矩形内接正三角形问题 思路
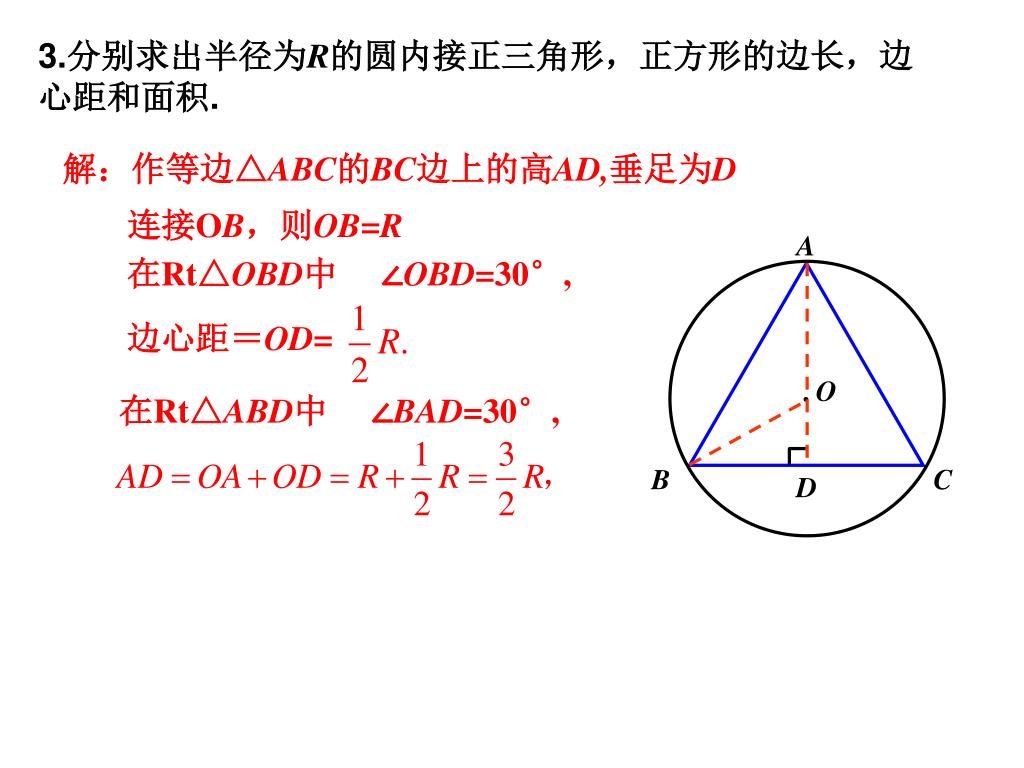



Ppt 24 3 1 正多边形和圆powerpoint Presentation Free Download Id




如何计算角度 8 步骤 包含图片



正三角形abc P是三角形内一点pa 3 Pb 4 Pc 5 求角apb的角度初中数学难题 哔哩哔哩 つロ干杯 Bilibili
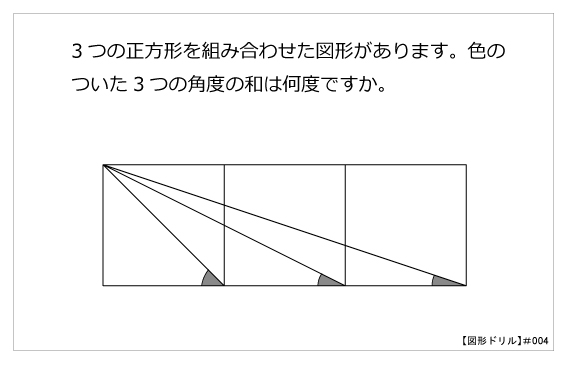



図形ドリル 第4問 正方形の角度 算数星人のweb問題集 中学受験算数の問題に挑戦




邊長為正整數且有一個角是60 或1 的三角形


